Dice Project - Finishing Up

Today We Discussed:

We used today's class to finish our discussion about probability, and to work on finishing projects.  All students are encouraged to type their conclusions using Google Docs.  Reminder, the finished project should include the following items:

• Rubric
• Printout of Data from 3 Trials of Rolling Dice
• Summary of Trial Data
• Frequency Tables (4)
• Theoretical Outcomes
• Histogram Containing 3 Trials
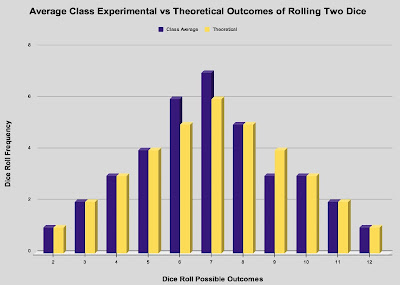
• Histogram of Trial Averages vs Theoretical Outcomes
• ThinkSheet
• Written Conclusion (Typed preferred)

Ms. Dause worked with students during study hall on how to effectively write a project conclusion.  

Sections Covered in Textbook:

None

Resources & Tutorials:

1) Project Packet (if needed)
2) Discussion Questions (if needed)

Dice Project - Chart Work Day

Today We Discussed:

We continued our progress with our dice project, and learned how to create new charts from our collected data.  For this project, we only focused on histograms/bar charts/column charts.  The completed project will have two histograms that are outlined in the project packet.

We also reviewed some practical uses of spreadsheets to gain better understanding of how and why they are used.

Finally, we discussed some of the things we learned by completing this project.  Students were given a list of discussion questions that they should use to build their conclusion document to be included with the final project. We will spend some time in class tomorrow going over the discussion questions and comparing data with each other.  

Sections Covered in Textbook:

None

Resources & Tutorials:

1)  Class Notes:  How to Create Charts in GSheets.
2)  How to create a column chart in GSheets (Video).
3)  Dice Project Discussion Questions

Chapter 4 Review and Frequency Tables

Topics for Today:

Today we reviewed briefly for our test tomorrow on Chapter 4.

We also developed our sample space and learned how to use frequency tables to organize our theoretical and experimental data from our project.

We have a test tomorrow, and notebooks are due.

By Wednesday, you need to have all of your data tallied and totaled on your frequency tables.

Attached is a copy of the review sheet, and the answers. Good luck!

Sections Covered in Textbook:

No new sections covered.  

Resources & Tutorials:

1) Chapter 4 Review Sheet

2) Chapter 4 Review Sheet answers

Probability of Compound Events

Today We Discussed:

Today we discussed probability of compound events.  We reviewed what the word "compound" means (and in this case, it simply means more than one), and discussed the different types of compound events.  There are two types:  independent events and dependent events.  Independent events occur when the outcome of one event has no effect on the other (ex:  flipping a coin twice).  Dependent events occur when the outcome of the first event does have an effect on the event that comes after (ex:  taking a card from a deck of cards and keeping it, then taking another card).

The numeric probability of dependent events can be found by multiplying the theoretical probability of each event together.

For two independent events, P(A and B) = P(A) * P(B)
For two dependent events, P(A then B) = P(A) * P(B after A)

Vocabulary: independent events, dependent events

Sections Covered in Textbook:

4-6: Probability of Compound Events

Resources & Tutorials:

1) What are compound events?
2) How to determine if your events are independent or dependent.
3) How to find probability of independent events.
4) How to find probability of dependent events.

5) Probability of Compound Events notes

Applying Ratios to Probability

Today We Discussed:

Ratios can be used to express everyday activities, and we will be using them in the context of probability.  Probability simply is the chance that an event can occur.  We defined all of the terms associated with both theoretical and experimental probability, and talked about how to find a sample space and how that relates to probability.  Exploring experimental probability is a good way to demonstrate that what we expect to happen, does not always occur, and probability is just based upon how likely something is to occur, not a guarantee it will occur.

We will be investigating experimental probability more thoroughly in the next week.


Graphic Credit:  Online Math Learning

Vocabulary: probability, outcome, event, sample space, theoretical probability, experimental probability 

Sections Covered in Textbook:

4-5: Applying Ratios to Probability (pages 211-217)

Resources & Tutorials:

1) What is probability?
2) What is an outcome?
3) What is a sample space? 
4) How do you find the probability of a simple event?
5) What is experimental probability?
6) Math is Fun - Probability (not a video)
7) Applying Ratios to Probability Class notes

Percent of Change

Today We Discussed:

We continued the topic of percents in the context of percent of change.  We can have a positive percent of change (representing an increase) or a negative rate of change (representing a decrease).  To determine the percent of change, we have to compare how much something changed to its original quantity.  Percent of change is relative to the original value.

Vocabulary: percent of change, percent of increase, percent of decrease

Sections Covered in Textbook:

4-4: Percent of Change (pages 204-209)

Resources & Tutorials:

1) What is the percent of change?
2) How do you find percent of change?
3) How do you determine percent of increase or decrease?

4) Percent of Change Class notes

Proportions and Percent Equations

Today We Discussed:

We expanded our discussion of proportions to include the percent proportion.  We deconstructed the word per-cent to mean "out of 100".  We can solve percent problems using a proportion or using a percent equation with the percent expressed as a decimal.

This unit will continue to explore proportions and percents, and we'll take some time to review the conversions of fractions to decimals to percents and vice-versa.  Students will be encouraged to memorize the decimal equivalents of common fractions as a time-saver.  Normally I am not a big fan of memorization, unless it serves a useful purpose - memorizing common concepts (like divisibility rules, the quadratic formula, and common numbers) can be a big time-saver leaving more time for higher order problem solving.

As we continue to explore the relationships among decimals, fractions, and percents, I plan to expand our discussion to other proportions, like circles.  We will investigate some probability in this unit as well.

Vocabulary: percent proportion, percent equation

Sections Covered in Textbook:

4-3: Proportions and Percent Equations (pages 197-202)

Resources & Tutorials:

1) What is a percent proportion?
2) How do you use a proportion to find a whole?
3) How do you use a proportion to find what percent a part is of a whole?
4) How do you use a proportion to find part of a whole?
5) What is a percent equation?
6) More Percent Equation Links

7) Proportion and Percent Equations Notes

Ratio and Proportion

Today We Discussed:

We began our unit on solving and applying proportions today, and introduced/reviewed some important vocabulary, beginning with ratios.  A ratio is just a comparison of numbers by division.  Students have seen ratios ever since they began working with fractions.  When we talk about rates, we create a ratio of two numbers that have different units.  We have already seen rates this year, when dealing with uniform motion -  rate of speed (comparing a distance with how much time elapses). 

We also used conversion factors to convert rates.  A conversion factor is a rate that is equal to 1 (multiplicative identity states we can multiply by 1 and not change the identity of our number).   For example, a unit conversion would be 60 seconds per minute since 1 minute=60 seconds.

Finally, we used the means-extremes (cross products) property to solve proportions. 

Vocabulary: ratio, rate, unit rate, conversion factor, unit analysis, dimensional analysis, proportion, cross products

Sections Covered in Textbook:

4-1: Ratio and Proportion (pages 182-187)

Resources & Tutorials:

1) What is a ratio?
2) What are rates and unit rates?
3) What is dimensional or unit analysis?
4) What is a proportion?
5) How to solve a proportion by using cross products?

6) Ratio and Proportion Notes

Chapter 3 Review

Today We Discussed:

Today we reviewed the topics from Chapter 3 in preparation for our test on Thursday. 

Our chapter covered the following items:

• Inequalities
• Multi-step
• Compound (AND and OR)
• Graphing
• Absolute Value
• Equations
• Inequalities

The big "take-aways" from this chapter are:

• Equations have finite solutions; inequalities have infinite solutions.
• When multiplying or dividing an inequality by a negative, you must flip the inequality sign to keep the truth of the inequality.
• Absolute Value equations and inequalities have two cases: positive and negative
• Absolute Value Inequalities come in two forms
• Greater than inequalities generate OR compound inequalities
• Less than inequalities generate AND compound inequalities

Sections Covered in Textbook:

All of Chapter 3 (pages 132-172) 

Resources & Tutorials:

Chapter 3 Review

Chapter 3 Review Answers