Factoring Trinomials Part 1

Topics for Today:

Our discussion about factoring moved to factoring trinomials today.  We played a game called the "Product-Sum" game where we analyzed a set of two numbers to see what factors create both a product and a sum.  We then related this game to how we factor trinomials.  We will always be looking to create a product (answer to a multiplication problem) and a sum (answer to an addition problem) at the same time.  Notice the coefficient that precedes the first term is one.  We'll address scenarios where the leading coefficient is NOT one in a future lesson.

Sections Covered in Textbook:

9-5: Factoring Trinomials of the type ax² + bx + c (where a=1)
       (pages 481-485)

Resources & Tutorials:

1) How do you factor a trinomial?
2) How to factor quadratic equations.

Multiplying Binomial Special Cases

Topics for Today:

We expanded our discussion on multiplying binomials today to include some common patterns:  squaring sums, squaring differences, and the product of a sum and a difference.  For each of these cases, we can always use the distributive property or FOIL methods to expand the product; however, as with many aspects in mathematics, recognizing patterns can save a lot of time.

Sections Covered in Textbook:

9-4: Multiplying Special Cases (pages 474-479)

Resources & Tutorials:

1) What is the formula for the square of a sum?
2) What is the formula for the square of a difference?
3) What's formula for the product of a sum and a difference?

Multiplying Binomials

Topics for Today:

Our topic for today was multiplying polynomials.  We focused our time mostly on multiplying two binomials together (recall that a binomial is the sum or difference of two monomials).  We focused on the number of individual products to ensure we did not leave any steps out.  Most people are familiar with the FOIL method for multiplying two binomials:

Sections Covered in Textbook:

9-3: Multiplying Binomials (pages 467-472)

Resources & Tutorials:

1) Multiply Binomials using the Distributive Property
2) Multiply Binomials using the FOIL method
3) How to Multiply Trinomials 

Multiplying and Factoring Polynonials

Topics for Today:

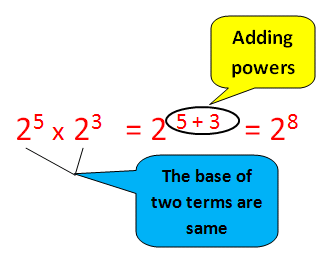
We explored multiplying a monomial by a polynomial today and doing the reverse by factoring out the greatest common factor.  Multiplying and factoring are inverse (opposite) operations of each other.

Vocabulary: Greatest Common Factor, GCF

Sections Covered in Textbook:

9-2: Multiplying and Factoring (pages 462-465)

Resources & Tutorials:

1) How do you multiply a monomial by a polynomial?
2) How do you find the Greatest Common Factor (GCF) of monomials?
3) Factoring Monomials from Polynomials

Adding and Subtracting Polynomials

Topics for Today:

Today we began our unit on polynomials with some definitions.  We also worked on adding and subtracting polynomials.  Like working with any variable expressions, we must always look for like terms when combining their components.  Variables raised to different powers cannot be combined by adding and subtracting.  One last concept to keep in mind is that when subtracting polynomials, you must subtract each piece of the polynomial; that is, the subtraction must be distributed to each piece of the polynomial and not just its first term.

Vocabulary:  monomial, degree of a monomial, polynomial, standard form of a polynomial, degree of a polynomial, binomial, trinomial

Sections Covered in Textbook:

9-1: Adding and Subtracting Polynomials (pages 456-461)

Resources & Tutorials:

1)  What is a monomial? 
2)  What is a polynomial? 
3)  How do you find the degree of a polynomial?
4)  How do you add polynomials? 
5)  How do you subtract polynomials? 

Division Properties of Exponents

Topics for Today:

Today we tackled the last property of exponents that deals with division.

When dividing powers with the same base, we can simply subtract the exponents.  When dividing monomials, we must match up like bases with each other, and deal with them separately.

Sections Covered in Textbook:

8-5: Division Property of Exponents (pages 417-423)

Resources & Tutorials:

1) What's the quotients of powers rule?
2) How do you divide monomials using the quotients of powers rule?
     (*This video leaves a negative exponent - that is NOT simplest form!*)

More Multiplication Properties of Exponents

Topics for Today:

Today we reviewed the topics relating to exponents and exponent rules, including scientific notation.  We expanded our topic of multiplication of powers to include raising a power to a power, as well as taking a monomial to a power.  When a monomial (a number, a variable, or a product of a number and variable - this also includes whole number exponents) is raised to a power, each element of that product must be raised to that power.

Sections Covered in Textbook:

8-4: More Multiplication Properties of Exponents (pages 411 - 415)

Resources & Tutorials:

1) What the power of a power rule?
2) How do you take a monomial to a power?
3) More on the power of a product rule.