Absolute Value Inequalities

Today We Discussed:

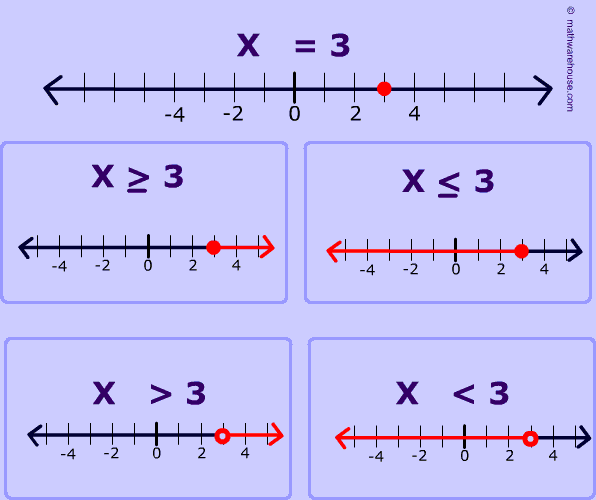
We continued our discussion about absolute value but moved on to inequalities.  Just like absolute value equations, we must consider TWO cases for absolute value inequalities - the positive case and the negative case.  Furthermore, we have to analyze which direction our solutions go based upon whether we are dealing with a greater than absolute value inequality or a less than absolute value inequality.

• Greater than absolute value inequalities function like OR compound inequalities.
• Less than absolute value inequalities function like AND compound inequalities.  

Graphic Credit: http://andymath.com/solving-absolute-value-inequalities/

Sections Covered in Textbook:

3-6: Absolute Value Equations and Inequalities (pages 167-171)

Resources & Tutorials:

1) How do you figure out if you have an AND or OR compound inequality?
2) How to solve an AND absolute value equation.
3) Introduction to Absolute Value Inequalities.
   (Use navigation on the left for more types of examples.)

4) Absolute Value Inequalities Notes

Assignments:

1) Absolute Value Inequalities Worksheet
2) Chapter 3 Test on Monday

Absolute Value Equations

Today We Discussed:

We moved into the next section in our book and discussed absolute value equations.  We will tackle absolute value inequalities on Thursday and Monday.

First, we reviewed absolute value and what it means - a number's positive distance from zero.  Absolute value equations add a small level of complexity because when we take the absolute value of a quantity, it will always be positive.   We can have an expression inside the absolute value bars be either positive OR negative, so we can end up with two solutions for the variable in these cases.

We must also analyze whether or not our absolute value equation makes sense.  In most cases, we will get two solutions, but there will be times when no solutions will be possible.  We need to make sure our equation is logical. 

Take for example the equation |x -2| = -3.   

There will never be a case when we take the absolute value of an expression that will result in a solution that is less than 0.  By its very definition, absolute value is always positive.  

For each of these absolute value equations, we will need to consider TWO cases for each solution set:  the positive case and the negative case. We will need to solve TWO equations to get the complete solution for the variable.

Sections Covered in Textbook:

3-6: Absolute Value Equations and Inequalities (pages 167-171)
(We will only cover equations today!)

Resources & Tutorials:

1) Four steps to solve absolute value equations. 
2) Introduction to absolute value equations.
3) Chili Math - Solving Absolute Value Equations (Not a video)

4) Absolute Value Equations Notes

Assignments:

1) Absolute Value Equations Worksheet
2) Quiz tomorrow on Solving Inequalities (7th)

Compound Inequalities

Topics for Today:

Our discussion about inequalities has moved on to compound inequalities.  We discussed the word "compound" and related it to compound words and compound sentences.  There are two types of compound inequalities:

• inequalities using OR 
• inequalities using AND. 

For the OR types, only part of the inequality needs to be true for the entire compound statement to be true.  For the AND types, we must have both parts true at the same time.  OR inequalities can be related to the UNION of two sets, and AND types represent the INTERSECTION (where both criteria are true at the same time).   Venn Diagrams (circle diagrams) are often used as pictorial representations of our sets. 

Sections Covered in Textbook:

3-5: Compound Inequalities (pages 161-165)

Resources & Tutorials:

1) What is a compound inequality?
2) How do you solve an OR compound inequality and graph it?
3) How do you solve an AND compound inequality and graph it?
4) How do you solve an AND compound inequality rewriting it as two?
5) What is a Venn Diagram?
6) Schoolhouse Rock - Conjunctions

7) Compound Inequalities Notes

Assignments:

1) Compound Inequalities Worksheet
2) Planning Ahead - Quiz Tuesday (7th) over Solving Inequalities

Solving Multistep Inequalities

Topics for Today:

We continue to build on our problem-solving skills with solving inequalities.  Today we moved on to more complicated inequalities that involve several steps.  Again, we approach these problems just like solving equations, with the first step being to identify the variable.  Once we identify the variable, we need to plan for how we "undo" operations performed on the variable with the goal of getting the variable by itself.  To accomplish this goal, we perform the order of operations (PEMDAS) in reverse.  *Students must always keep in mind that when multiplying or dividing an inequality by a negative number, they must reverse (flip) the inequality sign to keep the truth of the inequality.*

Sections Covered in Textbook:

Solving Multi-Step Inequalities (pages 153-159)

Resources & Tutorials:

1) How do you solve a multi-step inequality?
2) How do you solve an inequality with variables on both sides?
3) How to solve multi-step inequalities.

4) Solving Multi-Step Inequalities Notes

Assignments:

1)  Solving Multi-Step Inequalities Worksheet
2) Planning Ahead - Quiz Tuesday (Oct 27) over Inequalities (7th)

Solving Inequalities Using Multiplication and Division

Topics for Today:

Our discussion about solving inequalities moved to solving by using the multiplication and division properties of inequality.  We solve inequalities using the same steps and procedures as solving equations, but there is one notable exception.  For cases when we either multiply or divide both sides of our inequality by a negative number, we must switch the inequality sign to preserve the truth of the inequality.  To illustrate why this works, we did a little exploration with simple inequalities in class to help understand why the "truth" of an inequality changes.

Vocabulary: multiplication property of inequality, division property of inequality

We considered the following examples in class:

Sections Covered in Textbook:

3-3: Solving Inequalities Using Multiplication & Division
       (pages 146-151)

Resources & Tutorials:

1) What is the division property of inequality?
2) What is the multiplication property of inequality?
3)  Solving inequalities using multiplication and division
4) Virtual Nerd Page with more tutorials.

5)  Solving Inequalities Using Multiplication and Division Notes

Assignments:

1) Solving Inequalities Part II Worksheet

2) Chapter 2 Test Corrections due Wednesday (7th) or Thursday (8th)

Solving Inequalities Using Addition and Subtraction

Topics for Today:

Now that we understand what inequalities and solutions to inequalities are, we can now move into solving them.  When solving simple inequalities using addition and subtraction, we basically follow the same steps we use for solving simple equations.  For these problems, we will use the addition and subtraction properties of inequality to "undo" operations performed on a variable with the goal of getting the variable by itself.  Checking solutions to inequalities may not always locate our mistakes since there are an infinite number of possible solutions we can use to check ourselves.  Students will be encouraged to try out multiple possible solutions when checking.

Vocabulary: equivalent inequalities, addition property of inequality, subtraction property of inequality.

Graphic Credit:
https://www.mathwarehouse.com/number-lines/graph-inequality-on-number-line.php#examples1

Sections Covered in Textbook:

3-2: Solving Inequalities Using Addition and Subtraction (pages 140-144)

Resources & Tutorials:

1) What is the addition property of inequality? 
2) How do you solve an inequality using subtraction?
3) How do you solve an inequality using addition?

    (This includes putting the solution in set notation, which we did not discuss in class.)

4) Solving Inequalities Using Addition and Subtraction Notes

Assignments:

1) Chapter 2 Test Corrections Due Wednesday (7th) or Thursday (8th)

2) Solving Inequalities Part I Worksheet

Inequalities and Their Graphs

Topics for Today:

We moved on to Chapter 3 today.  Our discussion has moved from equations where both sides are equal, to inequalities where one side is larger or smaller than the other.  We also discussed the difference between solutions where the endpoint is included vs excluded and explored the graphs of inequalities.  A solution to an inequality is any value that will make the inequality true.  Inequalities differ from equations because inequalities often have infinite solutions that are bound by a particular value whereas equations typically have a finite solution set.

Graphic Credit: https://www.katesmathlessons.com/graphing-inequalities.html

Vocabulary: inequality, solution to an inequality

Sections Covered in Textbook:

3-1: Inequalities and Their Graphs (pages 134-138)

Resources & Tutorials:

1) What is an Inequality?
2) How Do You Graph Inequalities?
    (This video also includes infinite sets which we did not discuss.)

3) Inequalities and Their Graphs Class Notes

Assignments:

1) Inequalities and Their Graphs Worksheet

Chapter 2 Review - October 13/15

Topics for Today:

In preparation for our Chapter 2 test tomorrow, we spent the majority of our class working through practice problems.  Students should spend time tonight going through old homework and practicing solving and writing equations.  The test will cover solving one-step, two-step, and multi-step equations as well as equations with variables on both sides.  It will also cover problem solving with defining variables in terms of each other, consecutive number problems, break-even problems, and uniform motion (d=rt).

Study Skills:  Did you run out of problems to practice?  No problem!  Try working out the exercises at the end of each book section - there are example problems worked out in each section, and the homework problems are labeled in green to identify which practice problem is like the problem listed in the exercises.  The odd numbered problems have answers in the back so you can check to make sure you are solving the problems correctly!

Sections Covered in Textbook:

Chapter 2 Test will cover Sections 2-1 through 2-6 (Pages 74-115)

Resources & Tutorials:

1) Blog entry for One-Step Equations
2) Blog entry for Two-Step Equations
3) Blog entry for Multi-Step Equations
4) Blog entry for Variables on Both Sides of an Equation
5) Blog entry for Problem Solving Part 1 (break-even, consecutive numbers)
6) Blog entry for Problem Solving Part 2 (uniform motion)

7) Blog entry for Literal Equations
7) Answer Key for Chapter 2 Review Sheet

Assignments:

1) Chapter 2 Review Worksheet
2) Quiz Corrections due tomorrow (7th) or Thursday (8th)

3) Chapter 2 Test Tomorrow

Literal Equations - October 12/13

Topics for Today:

Welcome back, students!  Today we continued our exploration of equations, but focused on literal equations and formulas.  Literal equations are just equations that have more than one variable.  Formulas are mathematical or scientific facts, rules, or relationships expressed with mathematical symbols.  Students have been using formulas for much of their mathematics studies, although they may not be aware.  In the last chapter, we used the formula for distance (d=rt) and also perimeter of a rectangle {P=2(l+w)}.

We can use our knowledge of solving equations to move variables around in literal equations or formulas, to solve for a particular variable.  The properties of equality (addition, subtraction, multiplication, division and distributive) still apply here in these examples.

The first step in any solving equation problem it to identify the variable that you are solving for.  Once that is done, we follow the reverse order of operations to isolate the variable, and follow the same steps we used for solving multi-step equations.  As a reminder, here are those steps again:

Vocabulary: formula, literal equation

Sections Covered in Textbook:

2-6: Formulas (pages 111-114)

Resources & Tutorials:

1) What is a literal equation?
2) How do you solve a formula for a variable?
3) Summary of solving literal equations.

4) What did you forget over break class notes.

5) Literal Equations class notes

Assignments:

1) Literal Equations Worksheet

2) Quiz Corrections due Wednesday (7th) or Thursday (8th)

3) Chapter 2 Test Wednesday (7th) or Friday (8th)