Summary of Factoring

Topics for Today:

We have completed work in Chapter 9, and are reviewing all the concepts for factoring.  Students practiced decision-making, and which different processes we can use to factor polynomials. 

Next up - Review and Chapter 9 Test.  

Sections Covered in Textbook:

No new sections covered.

Resources & Tutorials:

1)  Factoring Decision Tree

Factoring Special Cases

Topics for Today:

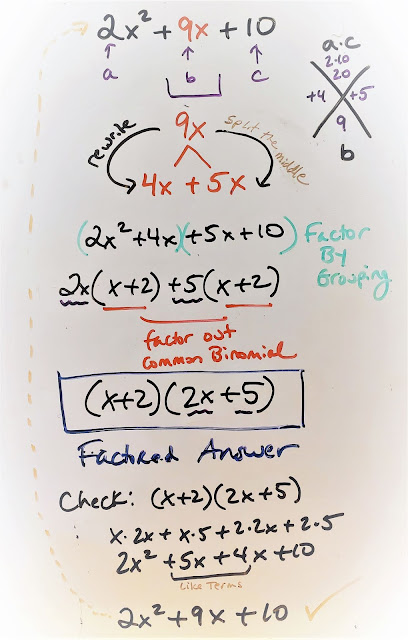
We are back to pattern recognition for factoring.  When we multiplied binomials by squaring them or by multiplying a difference, we noted a pattern for the resulting products.  Today, we worked backward from the trinomial (in the case of perfect square trinomials) or the binomial (in the case of difference of squares) to determine the two binomial factors. 

Students are reminded that now would be a good time to memorize the common perfect squares.  We also talked about square roots in the context of being the opposite of squaring numbers.  We'll deal with radicals a little later on, in May. 

For perfect square trinomials, students should be asking the questions:

• Is the first variable term a perfect square?
• If yes, is the constant term a perfect square?
• If yes, is the middle term equal to two times the square roots of the first and third terms?

What about factoring difference of squares?  We have another pattern to follow for this type of polynomial.  For the difference of squares, students should be asking the questions:

• Is the variable piece a perfect square?
• Is the constant piece a perfect square?
• Is the operation being performed subtraction?

Sections Covered in Textbook:

9-7: Factoring Special Cases

Resources & Tutorials:

1) How to use a shortcut to factor a perfect square trinomial
2) How do you factor using the difference of squares

Factoring Trinomials Part 2 - Split the Middle

Topics for Today:

We expanded our discussion today to include factoring polynomials where the leading coefficient is not 1.  We used the product-sum game to work with factors so we could "split the middle" of the equation, and then factor by grouping.

Sections Covered in Textbook:

9-6: Factoring Trinomials of the type ax² + bx + c (where a ≠ 1)

       (pages 486-489)

Resources & Tutorials:

1) Factor a trinomial using A-C method
    (This is a different method from what was introduced in class.)
2) Factor a trinomial with a > 1
    (This method is more like what was introduced in class.)

Factoring by Grouping

Topics for Today:

We continued our discussion of factoring polynomials today with a brief review of the Greatest Common Factor (GCF) and how we can divide the GCF out of a polynomial by using the distributive property in reverse.

Over the next several days we will tackle factoring of many different scenarios.  Factoring by grouping is a method that is used to deal with polynomials that have more than three terms.  Most people are familiar with factoring trinomials (3-terms), so when we are faced with more factors, our options are limited for how we can proceed.

In factoring by grouping, we will take two sets of two terms and pull out/factor out a GCF.  The goal is to have a leftover quantity for both groups that match one another.  If we do get our desired outcome, then we can further factor out the quantity, leaving us with a product of two binomials.

Sections Covered in Textbook:

9-8:  Factoring by Grouping (pages 496-501)

Resources & Tutorials:

1) How do you factor a 4-term polynomial by grouping?
2) The easiest way to factor a polynomial with four terms by grouping.

Factoring Trinomials Part 1

Topics for Today:

Our discussion about factoring moved to factoring trinomials today.  We played a game called the "Product-Sum" game where we analyzed a set of two numbers to see what factors create both a product and a sum.  We then related this game to how we factor trinomials.  We will always be looking to create a product (answer to a multiplication problem) and a sum (answer to an addition problem) at the same time.  Notice the coefficient that precedes the first term is one.  We'll address scenarios where the leading coefficient is NOT one in a future lesson.

Sections Covered in Textbook:

9-5: Factoring Trinomials of the type ax² + bx + c (where a=1)
       (pages 481-485)

Resources & Tutorials:

1) How do you factor a trinomial?
2) How to factor quadratic equations.

Multiplying Binomial Special Cases

Topics for Today:

We expanded our discussion on multiplying binomials today to include some common patterns:  squaring sums, squaring differences, and the product of a sum and a difference.  For each of these cases, we can always use the distributive property or FOIL methods to expand the product; however, as with many aspects in mathematics, recognizing patterns can save a lot of time.

Sections Covered in Textbook:

9-4: Multiplying Special Cases (pages 474-479)

Resources & Tutorials:

1) What is the formula for the square of a sum?
2) What is the formula for the square of a difference?
3) What's formula for the product of a sum and a difference?

Multiplying Binomials

Topics for Today:

Our topic for today was multiplying polynomials.  We focused our time mostly on multiplying two binomials together (recall that a binomial is the sum or difference of two monomials).  We focused on the number of individual products to ensure we did not leave any steps out.  Most people are familiar with the FOIL method for multiplying two binomials:

Sections Covered in Textbook:

9-3: Multiplying Binomials (pages 467-472)

Resources & Tutorials:

1) Multiply Binomials using the Distributive Property
2) Multiply Binomials using the FOIL method
3) How to Multiply Trinomials 

Multiplying and Factoring Polynonials

Topics for Today:

We explored multiplying a monomial by a polynomial today and doing the reverse by factoring out the greatest common factor.  Multiplying and factoring are inverse (opposite) operations of each other.

Vocabulary: Greatest Common Factor, GCF

Sections Covered in Textbook:

9-2: Multiplying and Factoring (pages 462-465)

Resources & Tutorials:

1) How do you multiply a monomial by a polynomial?
2) How do you find the Greatest Common Factor (GCF) of monomials?
3) Factoring Monomials from Polynomials

Adding and Subtracting Polynomials

Topics for Today:

Today we began our unit on polynomials with some definitions.  We also worked on adding and subtracting polynomials.  Like working with any variable expressions, we must always look for like terms when combining their components.  Variables raised to different powers cannot be combined by adding and subtracting.  One last concept to keep in mind is that when subtracting polynomials, you must subtract each piece of the polynomial; that is, the subtraction must be distributed to each piece of the polynomial and not just its first term.

Vocabulary:  monomial, degree of a monomial, polynomial, standard form of a polynomial, degree of a polynomial, binomial, trinomial

Sections Covered in Textbook:

9-1: Adding and Subtracting Polynomials (pages 456-461)

Resources & Tutorials:

1)  What is a monomial? 
2)  What is a polynomial? 
3)  How do you find the degree of a polynomial?
4)  How do you add polynomials? 
5)  How do you subtract polynomials? 

Division Properties of Exponents

Topics for Today:

Today we tackled the last property of exponents that deals with division.

When dividing powers with the same base, we can simply subtract the exponents.  When dividing monomials, we must match up like bases with each other, and deal with them separately.

Sections Covered in Textbook:

8-5: Division Property of Exponents (pages 417-423)

Resources & Tutorials:

1) What's the quotients of powers rule?
2) How do you divide monomials using the quotients of powers rule?
     (*This video leaves a negative exponent - that is NOT simplest form!*)

More Multiplication Properties of Exponents

Topics for Today:

Today we reviewed the topics relating to exponents and exponent rules, including scientific notation.  We expanded our topic of multiplication of powers to include raising a power to a power, as well as taking a monomial to a power.  When a monomial (a number, a variable, or a product of a number and variable - this also includes whole number exponents) is raised to a power, each element of that product must be raised to that power.

Sections Covered in Textbook:

8-4: More Multiplication Properties of Exponents (pages 411 - 415)

Resources & Tutorials:

1) What the power of a power rule?
2) How do you take a monomial to a power?
3) More on the power of a product rule.

Multiplication Properties of Exponents

Topics for Today:

Today we discussed how to manage multiplying powers with the same base.  We looked at several examples as well as explored how to multiply numbers together that are in scientific notation.  In summary, when multiplying powers with the same base, just keep the base and add the exponents together.  This process works for both positive and negative exponents.

Graphic Credit: https://www.onlinemath4all.com/multiply-powers.html

Sections Covered in Textbook:

8-3: Multiplication Properties of Exponents (pages 405-410)

Resources & Tutorials:

1) What is the product of powers rule? 
2) How do you find the product of powers? 
3) How do you multiply numbers using scientific notation? 

Scientific Notation

Topics for Today:

Today we used exponents in a practical way when we learned about scientific notation.  Scientific notation is simply a way to write very large and very small numbers that follow a few rules.

Simply stated, scientific notation is the product of a number and a power of 10 that follows the format: 

a x 10ⁿ  where n is an integer and 1 ≤ a < 10

Image credit: https://pt.slideshare.net/jessicagarcia62/compute-with-scientific-notation/6?smtNoRedir=1

Vocabulary:  scientific notation

Sections Covered in Textbook:

8-2: Scientific Notation (pages 400-404)

Resources & Tutorials:

1) What's scientific notation? 
2)  How do you convert decimal notation to scientific notation? 
3) How do you convert from scientific notation to decimal notation? 
4) How do you order numbers in scientific notation? 

Zero and Negative Exponents

Topics for Today:

We began a discussion about powers, bases and exponents today, and focused on bases with a zero exponent as well as negative exponents.

Summary

• Any non-zero number raised to the zero power equals one!
• Negative exponents are fractions.  If a factor is moved up or down in a fraction, the sign of the exponent is changed.  

Sections Covered in Textbook:

8-1: Zero and Negative Exponents (pages 394-399)

Resources & Tutorials:

1) What do you do with a zero exponent? 
2) What do you do with a negative exponent?